Statistik verstehen

Es gibt die Menschen, die es mit der Mathematik nicht so haben. Ich weiß das, denn ich unterrichte einige davon im Studiengang Psychologie bzw. Wirtschaftspsychologie an unterschiedlichen Universitäten und Hochschulen. Wäre es mir egal, könnt‘ ich’s mir oft einfacher machen. Aber ich bin der Meinung, dass Statistikkenntnisse enorm hilfreich und absolut praxisrelevant sind und versuche meinen Studierenden dies auch immer wieder zu verdeutlichen.

Deswegen ist es mir heute einen Blog-Beitrag wert, über ein paar sehr nützliche und gelungene Visualisierungen in d3.js (Data Driven Documents) von Kristoffer Magnusson zu berichten. Dem einen oder anderen mag es helfen, verschüttetes Statistikwissen aufzufrischen. Wirklich tolle Arbeit – sehr schön! Dies sind meine Highlights – weitere findet der interessierte Leser in Kristoffers Blog. Wie es aussieht wird die Liste immer weiter ergänzt.

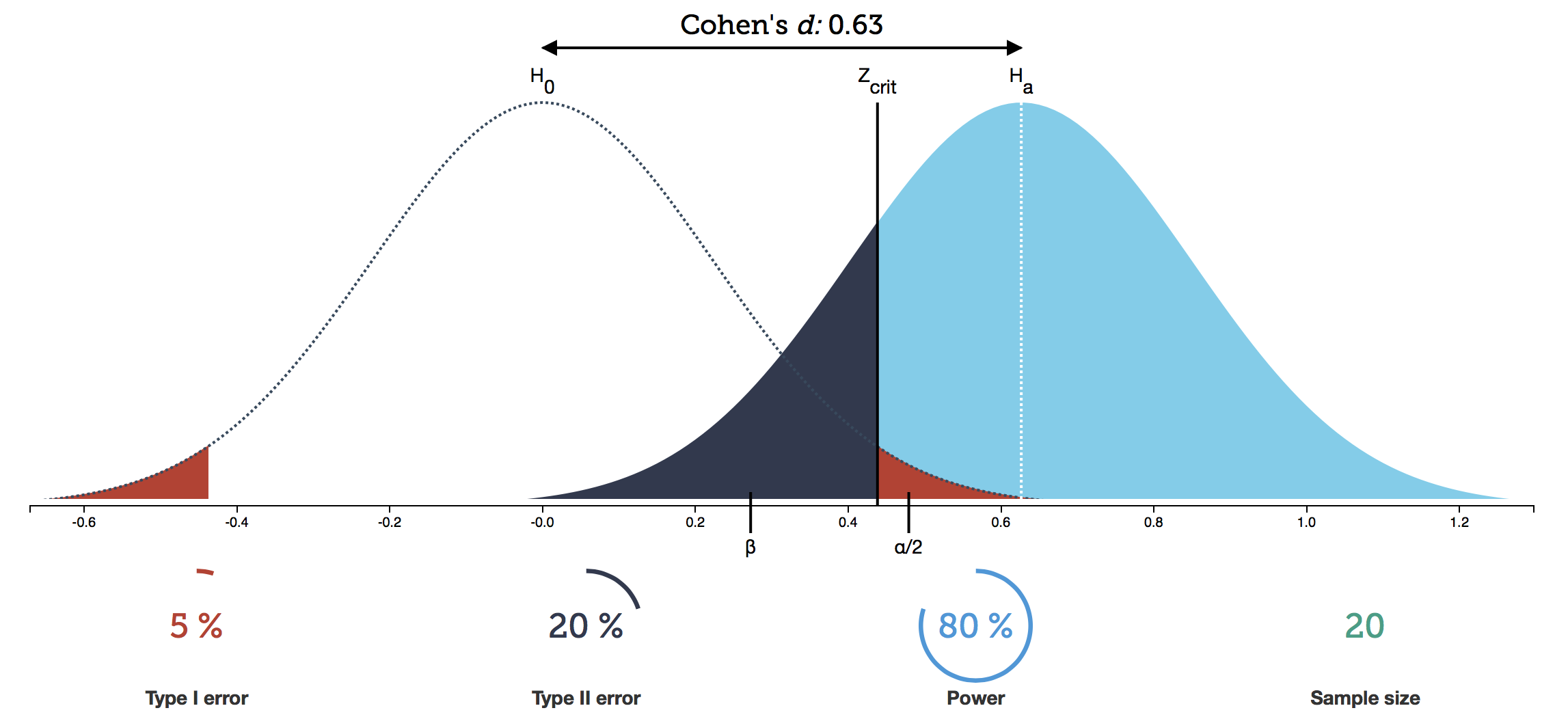
Der t-Test ist ein Signifikanztests, mit dem die Ablehnung der – die Gleichheit besagende – Nullhypothese nachgewiesen wird. Diese interaktive Grafik hilft beim Verständnis der Zusammenhänge zwischen zentralen Werten wie α- und β-Fehlern, Effektstärke und Stichprobengröße. Man kann die Werte beliebig verändern und sieht unmittelbar die Auswirkungen auf die jeweils abhängigen Größen.

Nicht auf Unterschiedlichkeit, sondern auf Gleichheit prüft der Äquivalenteste. So soll z.B. gezeigt werden, dass eine kostengünstigere Personalauswahlmethode genauso gut ist wie eine kostenintensive oder dass sich ein bestimmtes Merkmal in zwei Gruppen nicht unterscheidet. Die interaktive Erklär-Grafik findet man hier.

Ein Konfidenzintervall ist ein Bereich von Werten, der statistisch aus einer Stichprobe abgeleitet wurde und wahrscheinlich den Wert eines unbekannten Parameters der Grundgesamtheit (den sogenannten wahren Wert) umfasst. Ein häufig verwendetes Konfidenzniveau ist 95 %, so dass in diesem Fall (mindestens) 95 % aller auf Grundlage von gemessenen Daten berechneten Konfidenzintervalle den wahren Wert der zu untersuchenden Population beinhalten. Animation: hier.

Abschließend folgt noch das statistische Maß für die Enge eines Zusammenhangs zwischen zwei Merkmalen. Zum Beispiel kann der Zusammenhang zwischen Abiturnote (x-Achse) und allgemeiner Intelligenz (y-Achse) visualisiert werden. Für die Mathematiknote wird diese Korrelation immer wieder mit ungefähr r=.30 angegeben. Die Visualisierung zeigt sehr eindringlich, wie ungeeignet ein so geringer Zusammenhang im Einzelfall für die Vorhersage des einen Merkmals aufgrund der Kenntnis des anderen geeignet ist.